LEI DE HOOKE

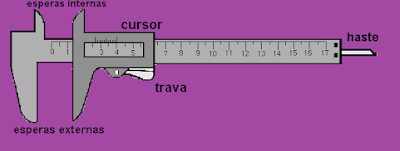
Imagem extraída de Augusto

A Força Elástica

A lei da Física que se relaciona à elasticidade de corpos, isto é, à deformação causada pela força exercida sobre um corpo é conhecida como Lei de Hooke, em homenagem ao cientista inglês Robert Hooke (1635-1703) que é um dos ícones da Revolução Científica. A Força Elástica é expressa por:

                                OBJETIVOS:

Medir grandezas físicas diretas e verificar experimentalmente a lei de hooke em molas helicoidais.

        FUNDAMENTOS TEÓRICOS USADOS:

     Quando forças externas atuam em um corpo sólido, a deformação resultante do corpo depende da extensão do material, da direção e do tipo de força aplicada.

MONTAGEM EXPERIMENTAL:

                          EXPERIÊNCIA:

a)    AJUSTAR O VALOR DE ZERO DA ESCALA DE MEDIDA COM UM PONTO DE REFERÊNCIA NA MOLA.

b)   ACRESCENTAR UMA MASSA NO PORTA MASSA E MEDIR A ELONGAÇÃO.

c)       REPETIR O PROCEDIMENTO ANTERIOR 5 VEZES.

d)  ORGANIZAR OS VALORES OBTIDOS EM UMA TABELA, COM COLUNA PARA O ÍNDICE DA MEDIDA, O VALOR DA MASSA E SEU ERRO, O VALOR DA ELONGAÇÃO E SEU ERRO.

REGISTRO DE DADOS
ESCALA VERTICAL	ESCALA HORIZONTAL
PESO SUSPENSO (N)	COMPRIMENTO DA MOLA (mm)
P0=0,00	X0=108,0±0,5
P1=0,45±0,05	X1=132,0±0,5
P2=0,91±0,05	X2=146,0±0,5
P3=1,30±0,05	X3=170,0±0,5
P4=1,85±0,05	X4=205,0±0,5
P5=2,30±0,05	X5=223,0±0,5
P6=2,85±0,05	X6=249,0±0,5
Σy = 9,66	Σx = 1233,0
RESULTADOS OBTIDOS
2,85 N ----- 195,0 mm      X -------- 1 mm     X= 0,0095 ≈ 0,010 N Assim, a incerteza na vertical é   1 mm ------- 0,010N    X ------------ 0,05      X= 5 mm	249,0 mm ------- 195,0 mm         X ---------------- 1,0 mm    X= 1,2770 ≈ 1,3 mm Temos a incerteza na horizontal     1 mm --------- 1,3 mm             X ---------- 0,5 mm         X= 0,38 ≈ 0,4 mm
COEFICIENTE ANGULAR
INCERTEZA EM K
AJUSTE DE CURVAS PELO MÉTODO DOS  MÍNIMOS QUADRADOS

CONCLUSÕES:

Como o coeficiente angular k é igual a 20 N/m para todo valor obtido, então o período de oscilação de um sistema massa-mola é independente da amplitude para pequenas oscilações.

Experimento 2

GRANDEZAS MECÂNICAS

Micrômetro

MEDIDAS DE GRANDEZAS MECÂNICAS

             Objetivo do Experimento

                 O experimento tem por objetivo o manuseio do paquímetro e do micrômetro para determinar as medidas de comprimento, de área e de volume de corpos sólidos, bem como as medidas de espessuras de objetos finos, diâmetros internos e externos.

             Fundamentos Teóricos Usados:

Durante todo o experimento houve variação dos valores obtidos no processo de medições, isto é, como cada instrumento usado apresenta limitações de medida, ocorre propagação do erro nos resultados.Portanto, a Incerteza Propagada fundamenta o experimento.

Montagem Experimental:

Régua, Paquímetro e Micrômetro

Experiência:

         Para a realização do experimento foram usados: uma régua milimetrada, um paquímetro, um micrômetro e um paralelepípedo de madeira.

      Iniciou-se o processo com o manuseio da régua e em seguida do paquímetro. Nessas etapas foram tomadas 10 medidas individuais para cada dimensão do sólido. Por último, usando o micrômetro, foram tomadas 10 medidas individuais da base do sólido. Visto que, a dimensão correspondente à altura ultrapassa a capacidade de aferição do micrômetro. Todos os valores obtidos foram anotados em tabelas individuais e calculada a média para cada dimensão aferida.

Régua

Registro de Dados:

MEDIDAS COM RÉGUA a(mm) b(mm) c(mm) 1 12,8±0,5 12,5±0,5 38,9±0,5 2 12,5±0,5 12,1±0,5 39,0±0,5 3 12,5±0,5 12,0±0,5 38,9±0,5 4 12,8±0,5 12,0±0,5 39,0±0,5 5 12,8±0,5 12,1±0,5 39,0±0,5 6 12,5±0,5 12,1±0,5 38,9±0,5 7 12,5±0,5 12,8±0,5 39,0±0,5 8 12,8±0,5 12,9±0,5 39,0±0,5 9 12,9±0,5 12,1±0,5 38,9±0,5 10 12,9±0,5 12,5±0,5 39,0±0,5 MÉDIA 12,7±0,5 12,3±0,5 39,0±0,5
	MEDIDAS COM O PAQUÍMETRO a(mm) b(mm) c(mm) 1 13,40±0,05 13,70±0,05 39,60±0,05 2 13,45±0,05 13,60±0,05 39,60±0,05 3 13,50±0,05 13,65±0,05 39,55±0,05 4 13,40±0,05 13,60±0,05 39,65±0,05 5 13,40±0,05 13,65±0,05 39,60±0,05 6 13,40±0,05 13,60±0,05 39,60±0,05 7 13,40±0,05 13,70±0,05 39,60±0,05 8 13,40±0,05 13,65±0,05 39,65±0,05 9 13,40±0,05 13,60±0,05 39,65±0,05 10 13,40±0,05 13,70±0,05 39,60±0,05 MÉDIA 13,42±0,05 13,65±0,05 39,61±0,05

MEDIDAS COM O MICRÔMETRO
	a(mm)	b(mm)	######
1	13,380±0,005	13,399±0,005
2	13,291±0,005	13,418±0,005
3	13,325±0,005	13,440±0,005
4	13,340±0,005	13,000±0,005
5	13,290±0,005	13,363±0,005
6	13,300±0,005	13,140±0,005
7	13,270±0,005	13,449±0,005
8	13,325±0,005	13,468±0,005
9	13,318±0,005	13,067±0,005
10	13,290±0,005	13,378±0,005
MÉDIA	13,313±0,005	13,312±0,005

            Resultados Obtidos:

Com o uso da Régua

A_base = comprimento x largura ± ∫A_base = a∫_b + b∫_a

A_base = 12,7 x 12,3 ± (12,7 x 0,5) + (12,3 x 0,5)

A_base = 156,2 ± 6,4 + 6,2

A_base = 156,2 ± 12,6 mm²

V_{paralelepípedo}  = comprimento x largura x altura ± ∫_v = A_base ∫_h + h∫A_base

V_{paralelepípedo}  = 156,2 x 39 ± (156,2 x 0,5) + (39 x 12,6)

V_{paralelepípedo}  = 6091,8 ± 78,1 + 491,4

V_{paralelepípedo}  = 6091,8 ± 569,5 mm³

            

Com o uso do Paquímetro

A_base = 13,42 x 13,65 ± (13,42 x 0,05) + (13,65 x 0,05)

A_base = 183,18 ± 0,67 + 0,68

A_base = 183,18 ± 1,35 mm²

V_{paralelepípedo}  = 183,18 x 39,61 ± (183,18 x 0,05) + (39,61 x 1,35)

V_{paralelepípedo}  = 7255,76 ± 9,16 + 53,47

V_{paralelepípedo}  = 7255,76 ± 62,63 mm³

            

Com o uso do Micrômetro

A_base = 13,313 x 13,312 ± (13,313 x 0,05) + (13,312 x 0,05)

A_base = 177,223 ± 0,067 + 0,067

A_base = 177,223 ± 0,134 mm²

           Conclusões:

           Como o micrômetro apresenta unidade de medida de comprimento igual à milionésima parte do metro, então ele apresenta maior sensibilidade que o paquímetro na aferição de objetos. É claro que o valor (177,223±0,134mm²) obtido para a base do sólido, quando medido com o micrômetro, é muito próximo da média aritmética dos valores obtidos, da medição da base do sólido, quando medido com a régua (156,2±12,6mm²) e o paquímetro (183,18±1,35mm²). Sendo a média para mais:

Média₊ = (156,2 + 12,6) + (183,18 + 1,35) / 2 = 176,665

Paquímetro

experimento 1